ചാപ്റ്റര് 5 – ഡാര്ക്ക് മാറ്റര്
“ഡാര്ക്ക് മാറ്റര്” എന്ന് വിളിക്കുന്നത് എന്താണ് എന്നും എങ്ങനെയാണ് ഇതിന്റെ കണ്ടെത്തല് ഉണ്ടായത് എന്നുമെല്ലാം ഈ ചാപ്റ്ററില് നോക്കാം.
ഗാലക്സികളുടെ റൊട്ടേഷന് കര്വ്
1930കളില്, ഗാലക്സികളിലെ നക്ഷത്രങ്ങളുടെ ചലനങ്ങളെ പറ്റി പഠിക്കുകയായിരുന്നു ചില ആസ്ട്രോണമേര്സ്. അതില് ഒരു പ്രമുഖനായ ഒരു ഡച്ച് ആസ്ട്രോണമര് ആയിരുന്നു ജാന് ഹെന്ട്രിക് ഊര്ട്ട് (Jan Hendrik Oort). ഗാലക്സികളുടെ ചലനത്തില് ചില പൊരുത്തക്കേടുകള് ഉണ്ടെന്ന് ഊര്ട്ട്, 1932ല് കണ്ടെത്തി. പൊരുത്തക്കേട് എന്നുവെച്ചാല് അവ ചലന നിയമങ്ങള് അനുസരിക്കുന്നില്ല എന്ന്.
ഒരു വര്ഷത്തിനു ശേഷം, 1933ല്, ഗാലക്സി ക്ലസ്റ്ററുകളും ബിഹേവ് ചെയ്യുന്നതില് ചില ശരികേട് ഉണ്ടെന്നു സ്വിസ് ആസ്ട്രോണമര് ആയിരുന്ന ഫ്രിറ്റ്സ് സ്വിക്കി (Fritz Zwicky) നിരീക്ഷിച്ചു.
മാത്രവുമല്ല, വിറിയല് തിയറം (Virial theorem) എന്ന മാത്തമാറ്റിക്കല് തിയറം ഉപയോഗിച്ച് “dunkle materie” അഥവാ ഡാര്ക്ക് മാറ്റര് എന്ന് അദ്ദേഹം വിളിച്ച വസ്തുക്കളുടെ അസ്തിത്വം അനുമാനിച്ചു.
ഇക്കാലത്ത് ഗാലക്സികളുടെ മാസ് എന്നത് അതിന്റെ ലുമിനോസിറ്റിയില് നിന്നാണ് അനുമാനിച്ചിരുന്നത്. പക്ഷെ അത് അങ്ങനെ അല്ലാ എന്നും പ്രകാശവുമായി ഇന്ററാക്റ്റ് ചെയ്യാത്ത വസ്തുക്കള് കൂടി ചേര്ത്താലേ മൊത്തം ഗാലക്സികളുടെ മാസ് കൃത്യമായി കണക്കാക്കാന് ആകൂ എന്നും ഇതില് നിന്നും വാദിച്ചു. ഈ വാദങ്ങള് പിന്നീടു സ്ഥിതീകരിക്കുകയുണ്ടായി.
ഇതിനെ കുറിച്ച് മനസ്സിലാക്കാന്, ഒരു ഗ്രാവിറ്റെഷണല് ഫീല്ഡില് ഒരു ഒബ്ജെക്റ്റ് എങ്ങനെ ചലിക്കും എന്ന് നോക്കാം. ഉദാഹരണത്തിന് ഒരു നക്ഷത്രത്തിന് ചുറ്റും ഒരു ഗ്രഹം അല്ലെങ്കില് ഒരു ഗാലക്സിയിലെ ഒരു നക്ഷത്രം.
ഒരു ഗാലക്സി. ചുവന്ന നിറം മാസ് ഡിസ്ട്രിബ്യൂഷനെ കാണിക്കുന്നു. (അതായത്, മദ്ധ്യത്തില് ആണ് കൂടുതല് മാസ്)
കുറിപ്പ്: ഇത് ഇങ്ങനെ അല്ലാ എന്ന് ഇന്ന് നമുക്കറിയാം.
ഒരു നക്ഷത്രത്തെ പരിഗണിക്കാം (പച്ച).
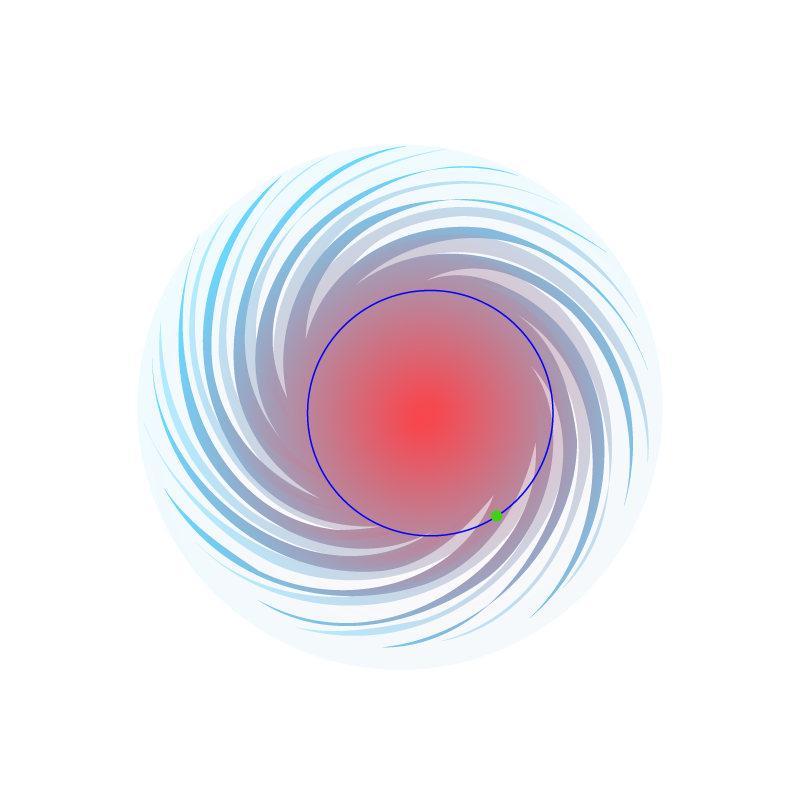
ഈ നക്ഷത്രം മദ്ധ്യത്തിലെ മാസ്സിന്റെ ചുറ്റും ഓര്ബിറ്റ് ചെയ്യുന്നു (നീല നിറത്തില് ഓര്ബിറ്റ്).
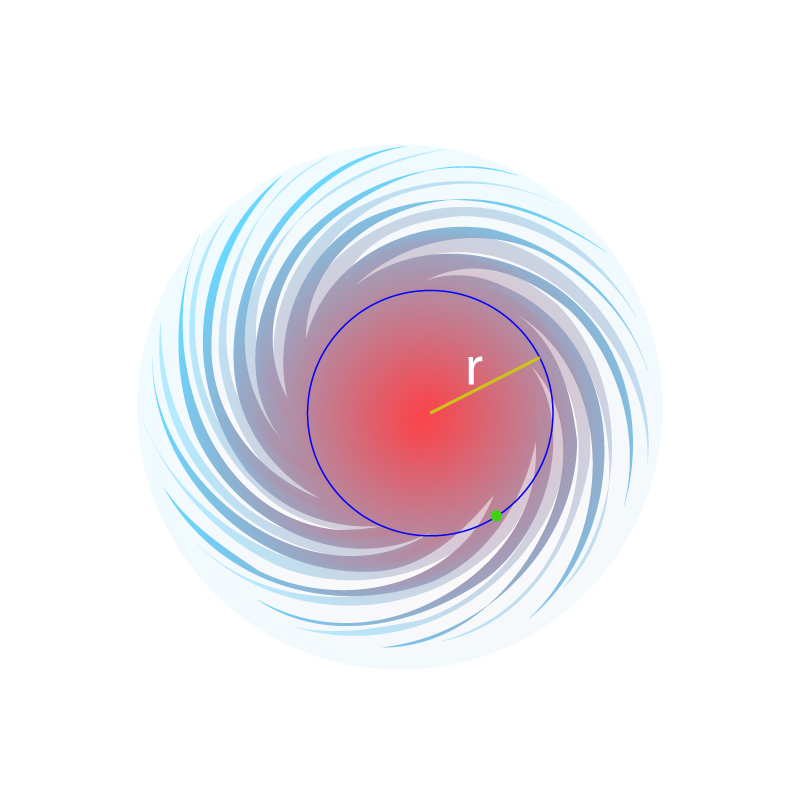
ഈ ഓര്ബിറ്റ്, മദ്ധ്യത്തില് നിന്നും \(r\) റേഡിയസ് അകലെ ആണ് എന്ന് വെക്കുക.
ന്യൂട്ടന്റെ \(F = ma\) സമവാക്യം ഉപയോഗിക്കാം.
ആ നക്ഷത്രത്തില്, മദ്ധ്യത്തിലെ മാസ് \(M\) മൂലം ഉണ്ടാകുന്ന ആക്സലറേഷന് \(a\) എന്നത്:
\[\frac{MG}{r^2} = a\]ആക്സലറേഷന് \(a\) എന്നത് \(\frac{v^2}{r}\) എന്നും എഴുതാം.
അപ്പോള്:
\[\frac{MG}{r^2} = \frac{v^2}{r}\]\(r\) കൊണ്ട് ഇരുവശവും ഗുണിച്ചാല്:
\[\frac{MG}{r} = v^2\]എന്നുവെച്ചാല്:
\[\sqrt{\frac{MG}{r}} = v\]അതായത്, വെലോസിറ്റി, \(\frac{1}{\sqrt{r}}\)ന് ആനുപാതികമായി കുറയുന്നു എന്ന്.
കുറിപ്പ്: ഇത്, കെപ്ലറുടെ പ്ലാനറ്ററി ചലന നിയമങ്ങളില് (Keplar’s laws of planetary motion) ഒന്നും രണ്ടും നിയമങ്ങളുടെ ജെനറലൈസേഷന് ആണ്.
ഇതിനെ ഒരു ഗ്രാഫില് ചിത്രീകരിച്ചാല് ഇങ്ങനെ ഇരിക്കും:
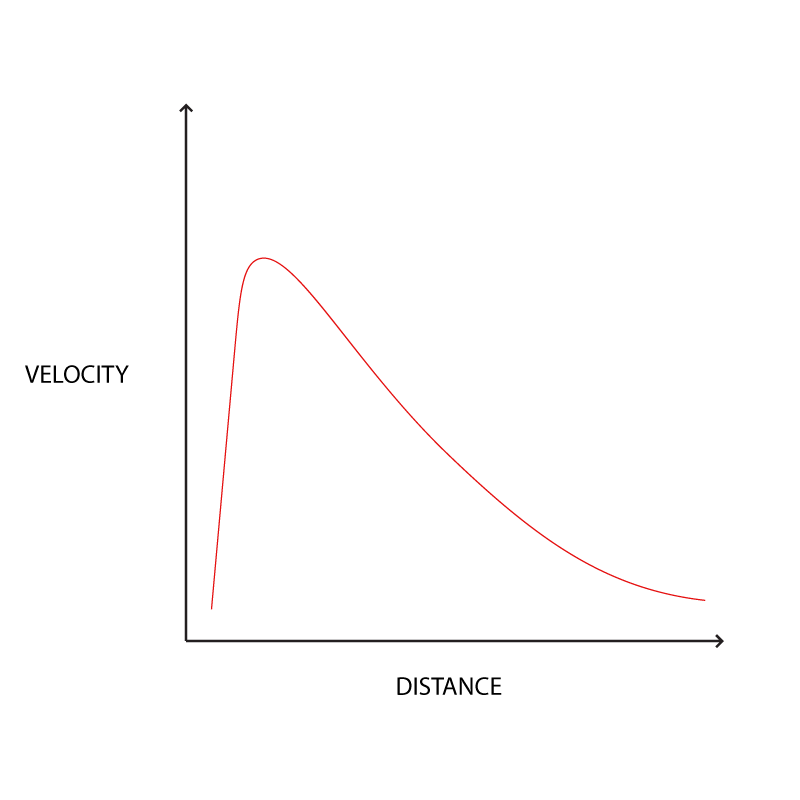
പക്ഷെ, ഊര്ട്ട്, ഫ്രിറ്റ്സ് സ്വിക്കി തുടങ്ങിയവര് കണ്ടെത്തിയ ബിഹേവിയര് ഇങ്ങനെ അല്ല. അത് താഴെ കാണുന്നപോലെ ആണ്:
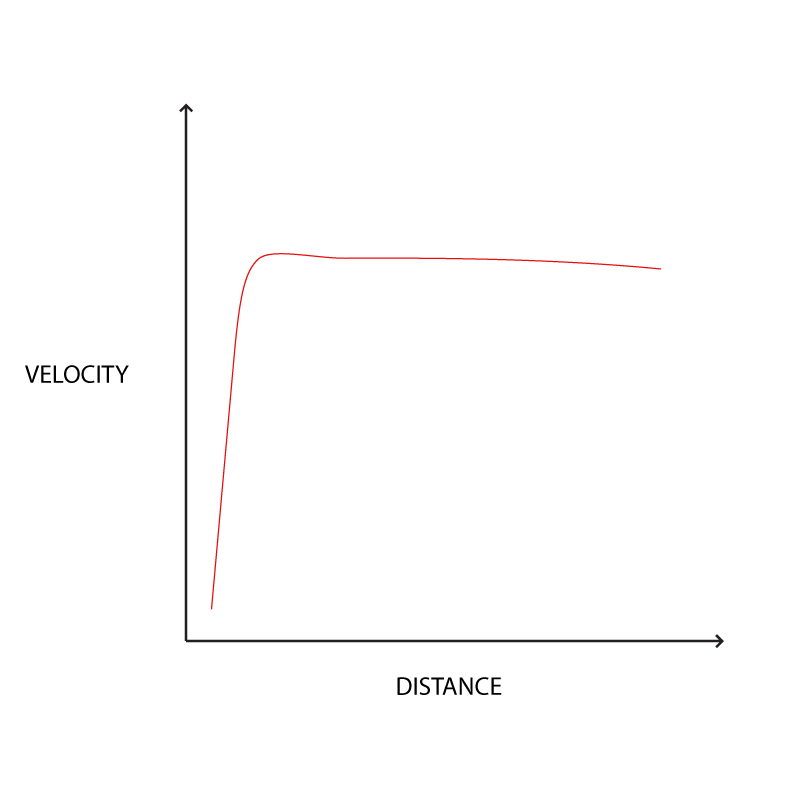
അതായത്, ഗാലക്സികളിലെ നക്ഷത്രങ്ങളുടെ ചലനം, മദ്ധ്യത്തില് നിന്നും അവ എത്ര അകലെയാണ് എന്നത് അനുസരിച്ചല്ല. മദ്ധ്യത്തില് നിന്നും എത്ര ദൂരത്തായാലും ഏകദേശം ഒരേ ഓര്ബിറ്റല് വെലോസിറ്റി ആകും അവയ്ക്ക്.
ഇങ്ങനെ സംഭവിക്കണമെങ്കില് രണ്ടു വഴിയേ ഉള്ളൂ.
- ചലന നിയമങ്ങള് ഗാലക്സികള്ക്ക് ബാധകമല്ല അഥവാ ചലന നിയമങ്ങള് ഗാലക്സികള്ക്ക് അപ്ലൈ ചെയ്യുമ്പോള് മോഡിഫൈ ചെയ്യണം.
- ഇലക്ട്രോ മാഗ്നറ്റിക് റേഡിയേഷന് ഉപയോഗിച്ച് നമുക്ക് കാണാന് സാധിക്കാത്ത മാസ് ഗാലക്സികളില് ഉണ്ട്.
ഇതില് ആദ്യത്തെ പോയിന്റ് അനുസരിച്ച് ചില മോഡലുകള് (മോഡിഫൈഡ് ന്യൂട്ടോണിയന് ഡൈനാമിക്സ്) നിര്മ്മിക്കപ്പെട്ടു എങ്കിലും അവ വിജയിച്ചില്ല.
കൂടുതല് നിരീക്ഷണങ്ങള്, രണ്ടാമത്തെ പോയിന്റ് ആണ് ശരി എന്ന് സ്ഥാപിച്ചു.
ഗ്രാവിറ്റെഷണല് ലെന്സിങ്ങ് എന്ന പ്രതിഭാസം ഉപയോഗിച്ച് ഗാലക്സികളിലെ മാസ് നിര്ണ്ണയിക്കാന് തുടങ്ങിയതോടെ ഡാര്ക്ക് മാറ്ററിന്റെ സാന്നിധ്യം കൂടുതല് വ്യക്തമായി.
ഗ്രാവിറ്റേഷണല് ലെന്സിങ്ങ്
ജനറല് ആപേക്ഷികത അനുസരിച്ച്, ഗ്രാവിറ്റി എന്നത് സ്പേസ്-ടൈമില് മാസ്/എനര്ജി ഡെന്സിറ്റി കാരണം ഉണ്ടാകുന്ന കര്വേച്ചറുകള് ആണ്.
കര്വ്ഡ് ആയ സ്പേസ്-ടൈമിലൂടെ സഞ്ചരിക്കുന്ന പ്രകാശത്തിന്റെ പാതയും അതിനനുസരിച്ച് “ബെന്ഡ്” ആകുന്നു.
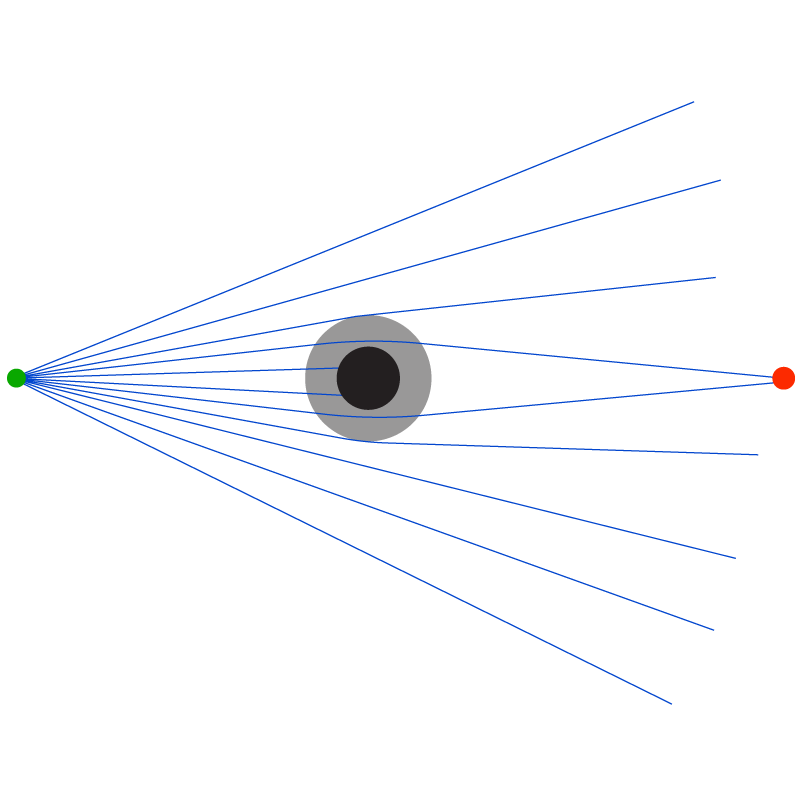
മുകളിലത്തെ ചിത്രത്തില്, ചുവന്ന ബിന്ദുവില് ആണ് നാം. പച്ച നിറത്തില് ഉള്ള പോയിന്റ് ഒരു വിദൂര ഗാലക്സി അഥവാ ലൈറ്റ് സോര്സ്. നീല നിറത്തില് പ്രകാശത്തിന്റെ രശ്മികള്. കറുത്ത നിറത്തില് ഉള്ളത് ഒരു വലിയ ഗ്രാവിറ്റേഷണല് ഒബ്ജെക്റ്റ് (ഉദാഹരണം: ഒരു ബ്ലാക്ക് ഹോള്). ചാര നിറത്തില് കാണുന്നത് ആ ഓബ്ജെക്റ്റിന്റെ ഗ്രാവിറ്റേഷണല് ഫീല്ഡിന്റെ പരിധി. ഈ ഗ്രാവിറ്റേഷണല് ഫീല്ഡിലൂടെ കടന്നുപോകുന്ന പ്രകാശ രശ്മികള് വളഞ്ഞു പോകുന്നത് ശ്രദ്ധിക്കുക.
പ്രകാശത്തിന്റെ പാതയില് വളരെയധികം മാസ് ഉണ്ടെങ്കില് അവ കാരണം സ്പേസ്-ടൈമില് ഉണ്ടാകുന്ന കര്വേച്ചറുകള് ഒരു ഒപ്റ്റിക്കല് ലെന്സ് പോലെ പ്രവര്ത്തിക്കുന്നു.
ഈ പ്രതിഭാസത്തെ ഗ്രാവിറ്റേഷണല് ലെന്സിങ്ങ് എന്ന് വിളിക്കുന്നു.
LRG 3-757 (Luminous Red Galaxy 3-757) എന്ന ഗാലക്സിയുടെ ഗ്രാവിറ്റേഷണല് ലെന്സിങ്ങ് കാരണം മറ്റൊരു വിദൂര ബ്ലൂ ഗാലക്സി ഒരു “റിംഗ്” ഷെയിപ്പില് കാണപ്പെടുന്നു. ഐന്സ്റ്റൈന് റിംഗ് എന്നാണു ഈ പ്രതിഭാസം അറിയപ്പെടുന്നത്. Credit: ESA/Hubble & NASA Hosted on Wikipedia
പ്രകാശ രശ്മികള് എന്തുമാത്രം വളയുന്നു എന്ന് നോക്കിയാല്, അവ സഞ്ചരിച്ച ഗ്രാവിറ്റേഷണല് ഫീല്ഡിന്റെ ശക്തി കണക്കാക്കാം. ഇതില് നിന്നും അവിടെ എന്തുമാത്രം മാസ് ഉണ്ട് എന്നും കണക്കാക്കാം.
2006ല്, ഡഗ്ലസ് ക്ലോവ് തുടങ്ങിയവര് നേതൃത്വം നല്കിയ ഒരു ഇന്റര്നാഷണല് കൊളാബറേഷന്, നാസയുടെ ചന്ദ്ര x-ray ഒബ്സര്വേറ്ററിയുടെ സഹായത്തോടെ നടത്തിയ നിരീക്ഷണങ്ങളുടെ ഫലമായി, ആസ്ട്രോ ഫിസിക്കല് ജേര്ണല് ലെറ്റേര്സില് ഒരു പേപ്പര് പബ്ലിഷ് ചെയ്തു (A Direct Empirical Proof of the Existence of Dark Matter, Douglas Clowe; et al. 2006, The Astrophysical Journal Letters). ഇതില് ഇവര് നിരീക്ഷിച്ചത് “ബുള്ളറ്റ് ക്ലസ്റ്റര്” എന്നറിയപ്പെടുന്ന ഒരു ഗാലക്സി ക്ലസ്റ്ററിനെ ആണ്.
ബുള്ളറ്റ് ക്ലസ്റ്റര് x-ray വഴി നോക്കുമ്പോള് ഇങ്ങനെ:

Credit: Chandra X-Ray Observatory - NASA, Hosted on Wikipedia
ഗ്രാവിറ്റേഷണല് ലെന്സിങ്ങ് ഉപയോഗിച്ച് മാസ് ഡിസ്ട്രിബ്യൂഷന് നീല നിറത്തില്:

രണ്ടു ഗാലക്സികള് കൂടിച്ചേര്ന്ന് ഉണ്ടായതാണ് ബുള്ളറ്റ് ക്ലസ്റ്റര്. പക്ഷെ ഈ ഗാലക്സി കളിലെ ബാരിയോണിക് മാറ്റര് (അതായത് സാധാരണമായ മാറ്റര്) മാത്രമാണ് കൂടിച്ചേര്ന്നത്. ഡാര്ക്ക് മാറ്റര് അതേ സ്ഥലത്ത് തന്നെ തുടര്ന്നു. ഇതിനു കാരണം ഡാര്ക്ക് മാറ്റര് വളരെ വീക്ക് ആയി മാത്രമേ ഇന്ററാക്റ്റ് ചെയ്യുള്ളൂ എന്നതാണ്.
ഈ ഗാലക്സികളുടെ കൊളിഷന് സിമുലേഷന്:
ഇന്ന് മറ്റു പല രീതിയിലും ഡാര്ക്ക് മാറ്ററിനെ ഡിറ്റെക്റ്റ് ചെയ്യാനുള്ള ടെക്നിക്കുകള് നിലവിലുണ്ട്.
FLRW (അ)സമ വാക്യം
ഇങ്ങനെ ഒരു തരം മാറ്ററിന്റെ കണ്ടെത്തല് കോസ്മോളജിസ്റ്റുകള്ക്ക് ഉപയോഗപ്രദമായി! കാരണം, ബാരിയോണിക് മാറ്റര് മാത്രം പരിഗണിച്ചാല് FLRW സമവാക്യത്തിന്റെ ഇരു വശവും യോജിക്കില്ല. ഇതെങ്ങിനെ എന്ന് നോക്കാം.
എന്താണ് FLRW സമവാക്യം പറയുന്നത്?
\[\left( \frac {\dot a}{a}\right)^2 = \frac {8}{3} \pi G \rho\]അതായത്, പ്രപഞ്ചത്തിലെ എനര്ജി ഡെന്സിറ്റി എന്നത് ഹബ്ബിള് കോണ്സ്റ്റന്റിന്റെ സ്ക്വയറിന് തുല്യം.
പ്രപഞ്ചത്തിന്റെ ജിയോമെട്രി കൂടി പരിഗണിച്ചാല്, വലതുവശത്ത് ഒരു ഘടകം കൂടി വരും:
\[\left( \frac {\dot a}{a}\right)^2 = \frac {8}{3} \pi G \rho - \frac {\kappa}{a^2}\]ഇനി, എനര്ജി ഡെന്സിറ്റി റോ (\( \rho\)) എന്നത് പല തരത്തിലുള്ളവയില് നിന്നാണ് ഉണ്ടാകുന്നത്:
\(C_R\) - റേഡിയേഷന്
\(C_M\) - മാറ്റര്
\(C_\Lambda\) - ഡാര്ക്ക് എനര്ജി
എന്നുവെച്ചാല് ചുരുക്കത്തില്:
\[C_R + C_M + C_\Lambda - C_\kappa = H^2\]ഇതിനെ പൊതുവേ മറ്റൊരു തരത്തില് എഴുതാറുണ്ട്: \(H\)ന്റെ റേഷിയോ ആയി:
\[\Omega_R + \Omega_M + \Omega_\Lambda + \Omega_\kappa = 1\]ഇവിടെ,
\(\Omega_R\) = \(\frac{C_R}{H^2}\)
\(\Omega_M\) = \(\frac{C_M}{H^2}\)
\(\Omega_\Lambda\) = \(\frac{C_\Lambda}{H^2}\)
\(\Omega_\kappa\) = \(\frac{C_\kappa}{H^2}\)
\(\Omega_R\) എന്നത് ഡയറക്റ്റ് ആയി ഓബ്സര്വ് ചെയ്യാന് സാധിക്കും. ഇന്ന് പ്രപഞ്ചത്തില് ഉള്ള റേഡിയേഷന്റെ ഭൂരിഭാഗവും കോസ്മിക് മൈക്രോവേവ് രൂപത്തില് ആണ്. ഇതിന്റെ വാല്യൂ മറ്റ് എനര്ജി ഡെന്സിറ്റികളെ അപേക്ഷിച്ച് വളരെ ചെറുതാണ്. ചിലപ്പോള് ഇതിനെ പരിഗണിക്കാറു പോലുമില്ല.
\(\Omega_M\) എന്നതും ഡയറക്റ്റ് ആയി ഓബ്സര്വ് ചെയ്യാന് സാധിക്കും. ഗ്രഹങ്ങള്, നക്ഷത്രങ്ങള്, ഗാലക്സികള്, ബ്ലാക്ക് ഹോളുകള് തുടങ്ങി സാധാരണമായി പ്രപഞ്ചത്തില് ഉള്ള വസ്തുക്കളാണ് ഇവ. ഇതിനെ ബാരിയോണിക് മാറ്റര് എന്ന് വിളിക്കുന്നു.
\(\Omega_\Lambda\) എന്നത് ഇന്ന് നമുക്ക് അറിയാമെങ്കിലും, 30 വര്ഷങ്ങള്ക്കു മുന്പ് ഇങ്ങനെ ഒരു ഘടകം ഈ സമവാക്യത്തില് ഉണ്ടായിരുന്നില്ല.
\(H\)ന്റെ വാല്യൂവും വളരെ കൃത്യമായി മെഷര് ചെയ്തിരുന്നു.
സമവാക്യം സമമാക്കനായി ബാക്കി വരുന്ന വാല്യു ആണ് \(\Omega_\kappa\) ആയി കണക്കാക്കിയിരുന്നത്.
അതായത്, 30 വര്ഷങ്ങള്ക്ക് മുന്പ് ഇതായിരുന്നു ഈ ഘടകങ്ങളുടെ വാല്യൂ:
\(\Omega_R \approx 0\) (ഇതിന്റെ ഡെന്സിറ്റി വളരെ ചെറുത്)
\(\Omega_M \approx 0.03 \) (ഒരു പ്രോട്ടോണ് പെര് ക്യുബിക് മീറ്റര്)
\(\Omega_\Lambda =0\) (ഇങ്ങനെ ഒരു ഘടകം അന്ന് പരിഗണിച്ചിരുന്നില്ല)
ഇവ എല്ലാം ചേര്ത്താല് വലതു ഭാഗത്തുള്ള 1ന് സമം ആകില്ല. ഇതില് നിന്നും കോസ്മോളജിസ്റ്റ്കള് അനുമാനിച്ചു പ്രപഞ്ചത്തിന്റെ ജിയോമെട്രി \(-1\) ആയിരിക്കണം എന്ന്.
അതായത്,
\[\frac{1}{a^2} \approx H^2\]\(H\)ന് വേറൊരു അര്ത്ഥം കൂടി ഉണ്ട് – പ്രപഞ്ചത്തിന്റെ പ്രായം. എങ്ങനെ?
ഉദാഹരണത്തിന്, മാറ്റര് ഡോമിനേറ്റ് ചെയ്യുന്ന മോഡല് എടുക്കാം (ചാപ്റ്റര് 3 കാണുക).
ഇതില്, \(a\)യുടെ വാല്യൂ നാം കണ്ടെത്തി:
\[a \approx t^{\frac{2}{3}}\]അപ്പോള്:
\[\frac{\dot a}{a} = \frac {2}{3} t^{\frac{-1}{2}} \; t^{\frac{-2}{3}} = \frac{2}{3t}\]അതായത്,
\[H = \frac{2}{3t}\]എന്നുവെച്ചാല് ഹബ്ബിള് കോണ്സ്റ്റന്റ് എന്നത് പ്രപഞ്ചത്തിന്റെ പ്രായത്തിന്റെ ഇന്വേര്സ് ആണ് എന്ന് അര്ത്ഥം:
\[H \approx \frac{1}{\text{age of the universe}}\]അപ്പോള്,
\[\frac{1}{a^2} \approx H^2 \approx \frac{1}{T^2}\]ഇവിടെ, \(T = \text{age of the universe}\)
(\(c=1\) ആയി അസ്സ്യൂം ചെയ്യുന്നു)
അതായത്, പ്രപഞ്ചത്തിന്റെ റേഡിയസ് എന്നത്, പ്രകാശം, പ്രപഞ്ചത്തിന്റെ പ്രായത്തിന് തുല്യമായി സഞ്ചരിക്കുന്ന ദൂരം ആണ് എന്ന്.
(ഇത് ഒട്ടുമേ ശരിയല്ല എന്ന് ഇന്ന് നമുക്കറിയാം).
ഇങ്ങനെ ഇരിക്കുമ്പോളാണ് ഡാര്ക്ക് മാറ്റര്, ഡാര്ക്ക് എനര്ജി എന്നിവയുടെ കണ്ടെത്തല്. ഇന്നത്തെ കോസ്മോളജിയില് താഴെ പറയുന്ന പോലെ ആണ് FLRW റേഷിയോകള്:
\[\Omega_R + \Omega_c + \Omega_b + \Omega_\Lambda + \Omega_\kappa = 1\]ഇവിടെ,
\( \Omega_c\) എന്നത് ഡാര്ക്ക് മാറ്റര് (Cold Dark Matter)
\( \Omega_b\) എന്നത് ബാരിയോണിക് മാറ്റര് (Baryonic Matter)
ഇവയുടെ വാല്യൂ എന്നത്, ഇന്നത്തെ കണക്കനുസരിച്ച്:
\(\Omega_R \approx 0 \)
\( \Omega_c = 0.275 \)
\( \Omega_b = 0.05 \)
\( \Omega_\Lambda = 0.675\)
\(\Omega_\kappa = 0\)
ഇവയുടെ വിവിധ വാല്യൂകള് ഇവിടെ ടെസ്റ്റ് ചെയ്യാം: സിഎംബി സിമുലേറ്റര്
“എന്താണ്” ഡാര്ക്ക് മാറ്റര്?
ഡാര്ക്ക് മാറ്റര് എന്നൊരു സംഭവം ഉണ്ട് എന്ന് നമുക്ക് ഇന്ന് അറിയാം. പക്ഷെ എന്താണ് ഇതിന്റെ ആന്തരിക സ്ട്രക്ചര്, എന്തുകൊണ്ട് ഇവ ഇന്ററാക്റ്റ് ചെയ്യുന്നില്ല എന്നൊന്നും നമുക്ക് വലിയ പിടിയില്ല.
എന്താണെന്ന് അറിയില്ല എങ്കിലും എന്തെല്ലാം അല്ലാ എന്ന് നമുക്ക് നല്ല നിശ്ചയമുണ്ട്. പാര്ടിക്ക്ള് ഫിസിക്സിന്റെ സ്റ്റാന്ഡേര്ഡ് മോഡലില് ഡാര്ക്ക് മാറ്റര് ആകാന് സാധ്യതയുള്ള പല പാര്ടിക്ക്ളുകളും ഉണ്ട്. ഡാര്ക്ക് മാറ്ററിന്റെ ബിഹേവിയര് അനുസരിച്ച് നോക്കുകയാണെങ്കില്, മാസ്സ്, ഇവ അനുസരിക്കുന്ന സ്റ്റാറ്റിസ്റ്റിക്സ് (ഫെര്മിയോണ്, ബോസോണ് തുടങ്ങിയവ) എന്ന് തുടങ്ങി പലതരം പരിധികളും ഇവക്കു ഉണ്ട്. ഇവയെല്ലാം ഒത്തുവരുന്ന പാര്ടിക്ക്ളുകള് പാര്ടിക്ക്ള് ഫിസിക്സിന്റെ സ്റ്റാന്ഡേര്ഡ് മോഡല് പ്രവചിക്കുന്നുണ്ട്. അവയില് ചിലത് ഇവയാണ്:
• വിംപ്സ് അഥവാ വീക്ക്ലി ഇന്ററാക്റ്റിങ്ങ് മാസ്സിവ് പാര്ടിക്ക്ള്സ് (Weakly Interacting Massive Particles – WIMPs)
ഏകദേശം ഹിഗ്സ് ബോസോണിന്റെ മാസ്സ് റേഞ്ചിന് സമീപം മാസ്സ് ഉള്ള ഒരുതരം ഹൈപ്പൊതെറ്റിക്കല് പാര്ടിക്ക്ള്സ് ആണ് വിംപ്സ്. സേണിന്റെ (CERN) ലാര്ജ് ഹാഡ്രോണ് കൊള്ളൈഡറില് (LHC) ഡിറ്റക്റ്റ് ചെയ്യപ്പെടും എന്ന് പ്രതീക്ഷിച്ചിരുന്നു എങ്കിലും ഇതുവരെ അങ്ങനെ ഒരു കണ്ടെത്തല് ഉണ്ടായിട്ടില്ല.
• സ്റ്റെറൈല് ന്യൂട്രീനോ (Sterile Neutrino)
ഇതുവരെ കണ്ടെത്തിയിട്ടില്ലാത്ത ഒരു തരം ന്യൂട്ട്രീനോ ടൈപ്പ് ആണ് ഇവ. സാധാരണ ന്യൂട്രീനോ ഫ്ലേവറുകള് (ഇലക്ട്രോണ് ന്യൂട്രീനോ ടൌ ന്യൂട്രീനോ, മ്യുവോണ് ന്യൂട്രീനോ) പോലെ ഇവയും ഫെര്മിയോണുകള് ആണ്. അതായത് ഇവ ഫെര്മി-ഡിറാക്ക് സ്റ്റാറ്റിസ്റ്റിക്സ്, പൌളി എക്സ്ക്ലൂഷന് പ്രിന്സിപ്ള് എന്നിവ പാലിക്കുന്നു. എന്നാല് മറ്റു ന്യൂട്ട്രീനോകളെ പോലെ വീക്ക് ഇന്ററാക്ഷന് സ്റ്റെറൈല് ന്യൂട്രീനോകള്ക്ക് ഇല്ല. ഇവ ഗ്രാവിറ്റെഷണല് ആയിട്ട് മാത്രമേ ഇന്ററാക്റ്റ് ചെയ്യുള്ളൂ.
• ആക്സിയോണുകള് (Axions)
\(10^{-5} \; \frac{eV}{c^2}\)നും \(10^{-3} \; \frac{eV}{c^2}\)നും ഇടയില് മാസ് ഉള്ള ഹൈപൊതെറ്റിക്കല് ബോസോണുകള് ആണ് ആക്സിയോണുകള്.
ഇന്നത്തെ നമ്മുടെ അറിവ് അനുസരിച്ച്, നമ്മുടെ പ്രപഞ്ചത്തില് ഉള്ള ഡാര്ക്ക് മാറ്റര് താഴെ പറയുന്ന പ്രത്യേകതകള് ഉള്ളവയാണ്:
• ഇവ റേഡിയേറ്റ് ചെയ്യുന്നില്ല (ഗ്രാവിറ്റെഷണല് റേഡിയേഷന് ഒഴിച്ചാല്), അതിനാല് തന്നെ ഇവയെ “ഡാര്ക്ക്” എന്ന് വിളിക്കുന്നു.
• ഇവക്ക് മാസ് ഉണ്ട്.
• ഇവ വളരെ പതുക്കെ മാത്രമേ ചലിക്കുന്നുള്ളൂ, അതിനാല് ഇവയെ “കോള്ഡ്” എന്ന് വിളിക്കുന്നു (വേഗത്തില് ചലിക്കുന്ന തരം ഡാര്ക്ക് മാറ്ററിനെ ഹോട്ട് ഡാര്ക്ക് മാറ്റര് എന്ന് വിളിക്കുന്നു).
• പ്രപഞ്ചത്തിന്റെ ഉള്ളടക്കത്തില് ഏകദേശം 27% വരുന്നത് ഡാര്ക്ക് മാറ്റര് ആണ് (മനുഷ്യരും, ജീവികളും, ഭൂമിയും, ഗ്രഹങ്ങളും, നക്ഷത്രങ്ങളും, ഗാലക്സികളും, തമോഗര്ത്തങ്ങളും എല്ലാം കൂടി 5% മാത്രമേ ഉള്ളൂ. ബാക്കി 68% വരുന്നത് ഡാര്ക്ക് എനര്ജിയാണ്).
• ഇവ പ്രപഞ്ചത്തില് കൂട്ടം കൂടി (clustering) കാണപ്പെടുന്നു.
• ഇവ ഗാലക്സികള്ക്ക് ചുറ്റും ഗോളാകൃതിയില് ഡിസ്ട്രിബ്യൂട്ട് ചെയ്യപ്പെട്ടിരിക്കുന്നു. സ്പൈറല് ഗാലക്സികളുടെ സ്പൈറല് ഷെയിപ്പ് ഇവ അനുസരിക്കുന്നില്ല.
• ഒറ്റപ്പെട്ട ഗാലക്സിളില് മാത്രമല്ല ഗാലക്സി ക്ലസ്റ്ററുകളിലും, സൂപ്പര് ക്ലസ്റ്ററുകളിലും ഇവയുടെ സാന്നിധ്യം സ്ഥിതീകരിച്ചിട്ടുണ്ട്.
ഗാലക്സികളുടെ ചുറ്റും കുമിഞ്ഞു കൂടി ആണ് ഡാര്ക്ക് മാറ്റര് ഇന്ന് കാണപ്പെടുന്നത് എങ്കിലും ഗാലക്സികളുടെ രൂപികരണത്തില് ഇത് നേരെ മറിച്ച് സംഭവിച്ചിരിക്കാനാണ് സാധ്യത.
അതായത്, ഡാര്ക്ക് മാറ്റര് കുമിഞ്ഞു കൂടി ഉണ്ടായ ഗ്രാവിറ്റെഷണല് വെല്ലിന് (Gravitational well) ഉള്ളിലേക്ക് വീണ ബാരിയോണിക് മാറ്റര് പരിണമിച്ചുണ്ടായതാകാം ഗാലക്സികള്.
എല്ലാ ഗാലക്സികള്ക്ക് ചുറ്റും ഡാര്ക്ക് മാറ്റര് കാണപ്പെടണം എന്നില്ല. ഈ അടുത്ത ഇടക്ക്, ഡാര്ക്ക് മാറ്റര് ഇല്ലാത്ത ചില ഗാലക്സികള് കണ്ടെത്തുകയുണ്ടായി. (Source)