ചാപ്റ്റര് 2: മാസ്/എനര്ജി ഡെന്സിറ്റിയും ഫ്രീഡ്മന് സമവാക്യവും – ന്യൂട്ടണില് നിന്നും.
ഫ്രീഡ്മന് സമവാക്യം എന്ന് ഇവിടെ വിളിക്കുന്നു എങ്കിലും, ഇതിനെ പൊതുവേ മറ്റു പേരുകളിലും അറിയപ്പെടുന്നു - FRW സമവാക്യം (ഫ്രീഡ്മന്-റോബേര്ട്ട്സണ്-വാക്കര് എന്നിവരുടെ പേരില് നിന്നും), FLRW സമവാക്യം (ഫ്രീഡ്മന്-ലമാത്രെ-റോബേര്ട്ട്സണ്-വാക്കര് എന്നിവരുടെ പേരില് നിന്നും)
ഇനി നമുക്ക് ഒരു കാര്യം ചോദിക്കാം: നാം നിര്മ്മിച്ച ഈ ഗ്രിഡില് ഒരു നിശ്ചിത റീജിയണിനു ഉള്ളില് എന്തുമാത്രം മാസ് ഉണ്ടാകും?
ഉത്തരം \(\Delta x \Delta y \ \Delta z\) ക്ക് ആനുപാതികം ആയിരിക്കും.
ഒരു നിശ്ചിത യൂണിറ്റ് വോള്യം ഗ്രിഡില് ഉള്ള മാസ്സിനെ നമുക്ക് ഗ്രീക്ക് ലെറ്റര് നൂ \(\nu\) എന്ന് വിളിക്കാം. ഈ വോള്യം മീറ്ററില് അല്ല \(x\)ല് ആണ് അളക്കുന്നത്.
അതായത് മാസ് \(M\) എന്ന് പറയുന്നത്:
\[M= \nu \Delta x \Delta y \Delta z\]അപ്പോള് വോള്യം \(V\):
\[V= a^3 \Delta x \Delta y \Delta z\]അപ്പോള് മാസ് ഡെന്സിറ്റിയോ?
ഡെന്സിറ്റി \(\rho\) (റോ) \(M,V\) എന്നിവയുടെ റേഷിയോ ആണ്:
\[\rho=\frac{M}{V}\]അതായത്,
\[\rho=\frac{\nu}{a^3}\]\(\Delta x \Delta y \Delta z\) ക്യാന്സല് ആയത് ശ്രദ്ധിക്കുക
ഇതില് നിന്നും എന്ത് മനസ്സിലാക്കാം?
ഒരു നിശ്ചിത റീജിയണിനുള്ളില് ഉള്ള മാസ് കോണ്സ്റ്റന്റ് ആയി നിലനില്ക്കും.
എന്തുകൊണ്ട്? കാരണം നമ്മുടെ ഗ്രിഡ് ഗാലക്സികള്ക്ക് അനുസരിച്ച് മൂവ് ചെയ്യും.
മുകളില് പറഞ്ഞ സമവാക്യത്തില് a എന്നത് സമയത്തിന് അനുസരിച്ച് മാറുന്ന ഘടകമാണ്. അതിനാല് ഡെന്സിറ്റിയും സമയത്തിനനുസരിച്ച് മാറുന്നു.
നമ്മള് ഈ ഗ്രിഡിന്റെ മദ്ധ്യത്തില് അല്ലെങ്കില് ഒറിജിനില് ആണെന്ന് വെക്കുക, ചിത്രത്തില് കാണുന്ന പോലെ:

നമ്മള് റസ്റ്റ് പൊസിഷനില് ആണെന്നും കരുതുക. അതായത് നാം മൂവ് ചെയ്യുന്നില്ല.
ഏതെങ്കിലും ഒരു വിദൂര ഗാലക്സിയെ പരിഗണിക്കാം:

ആ ഗാലക്സി എങ്ങനെയാണ് സഞ്ചരിക്കുന്നത് എന്ന് നമുക്ക് അറിയണം. ഈ മോഷന് ന്യൂട്ടണ് നിയമങ്ങള്ക്ക് അനുശ്രിതമായി ആയിരിക്കും എന്ന് നമുക്ക് അറിയാം.
പക്ഷെ ഈ ചിത്രം നോക്കുകയാണെങ്കില് ആ ഗാലക്സിയുടെ മോഷന് കണക്കാക്കുക വലിയ മെനക്കെട്ട പരിപാടി ആണെന്ന് തോന്നും.
നമുക്കും ആ ഗാലക്സിയ്ക്കും ഇടയില് ഒരുപാട് മറ്റു ഗാലക്സികള് ഉണ്ട്.
നമ്മള് പരിഗണിക്കുന്ന ഗാലക്സിയ്ക്ക് ചുറ്റും വേറെ ഗാലക്സികല് ഉണ്ട്.
ഇവയെല്ലാം നമുക്ക് പരിഗണിച്ചല്ലേ പറ്റൂ? ഇവയെല്ലാം ആ ഗാലക്സിയുടെ മോഷനെ ബാധിക്കില്ലേ?
ഇവിടെ നമുക്ക് ഒരു തിയറം ഗുണകരമാകും.
തിയറത്തിന്റെ പേര് ഷെല് തിയറം അഥവാ ന്യൂട്ടണ്സ് തിയറം (ഐസക് ന്യൂട്ടണ് 1687ല് ഇത് പ്രൂവ് ചെയ്തു).
ഷെല് തിയറം അനുസരിച്ച്, ഒരു ഐസോട്രോപിക്ക് സിസ്റ്റത്തിലെ ഒരു പാര്ടിക്ക്ളിന്റെ മോഷന് കണക്കാക്കണമെങ്കില് മൂന്നു കാര്യങ്ങള് ചെയ്യുക:
-
കോര്ഡിനേറ്റ് സിസ്റ്റത്തിന്റെ മദ്ധ്യത്തില് ഉള്ള നമ്മളില് നിന്നും നാം പരിഗണിക്കുന്ന പാര്ടിക്ക്ളിനെ ബൌണ്ടറിയില് വരുന്ന രീതിയില് ഒരു വൃത്തം അല്ലെങ്കില് സ്ഫിയര് വരക്കുക:
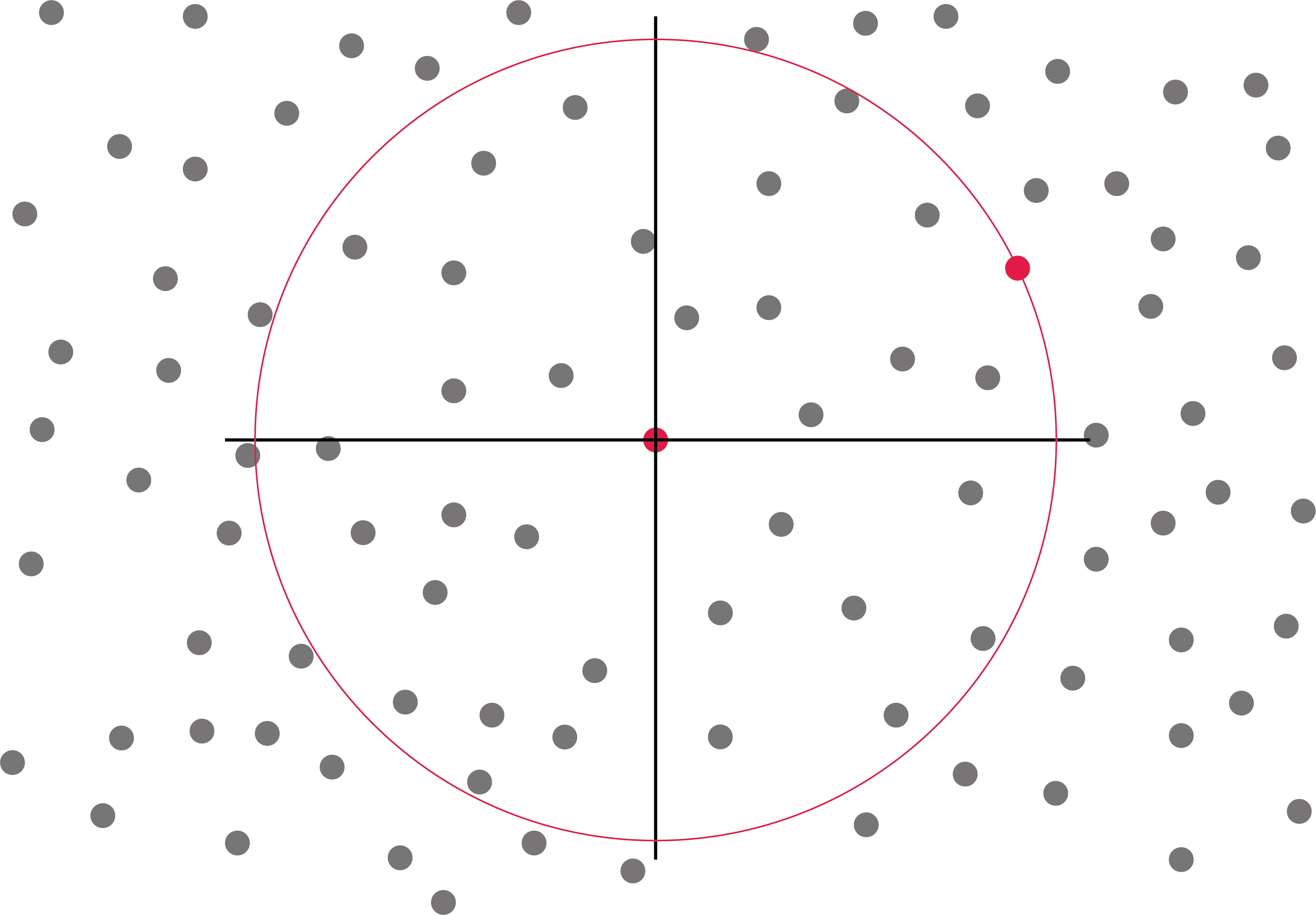
-
ഈ സ്ഫിയറിനുള്ളില് ഉള്ള എല്ലാ മാസ്സും ഒറിജിന് പോയിന്റില് കേന്ദ്രീകരിക്കുന്നതായി സങ്കല്പ്പിക്കുക:

-
ഈ സ്ഫിയറിനു പുറത്തുള്ള എല്ലാ മാസ്സും അവഗണിക്കുക.

ചുരുക്കത്തില്:
ഒറിജിന് പോയിന്റും പാര്ടിക്ക്ളും തമ്മിലുള്ള ദൂരം:
\[D=a(t)\sqrt{x^2+y^2+z^2}\]\(\sqrt{x^2+y^2+z^2}\)നെ നമുക്ക് \(R\) എന്ന് വിളിക്കാം. അപ്പോള്:
\[D=a(t) R\]ന്യൂട്ടന്റെ സമവാക്യങ്ങള് ഫോര്സുകളെകുറിച്ചും ആക്സലറേഷനെ കുറിച്ചും ഉള്ളതാണ്.
അതിനാല് നമുക്ക് ഒറിജിന് പോയിന്റിനെ അപേക്ഷിച്ചുള്ള ഈ പാര്ടിക്ക്ളിന്റെ അഥവാ ഗാലക്സിയുടെ ആക്സലറേഷന് കണക്കാക്കാം.
ആദ്യം വെലോസിറ്റി:
\[V=\dot a(t) R\](വെലോസിറ്റി എന്നത് പൊസിഷന് ഫങ്ങ്ഷന്റെ ഒന്നാം ഡെറിവെറ്റിവ് ആണ് എന്ന് ഓര്ക്കുക. അതായത് Dയുടെ ഒന്നാം ഡെറിവെറ്റിവ്.)
അപ്പോള് ആക്സലറേഷന്:
\[A=\ddot a(t) R\](ആക്സലറേഷന് എന്നത് പൊസിഷന് ഫങ്ങ്ഷന്റെ രണ്ടാം ഡെറിവെറ്റിവ് ആണ്; അഥവാ വെലോസിറ്റിയുടെ ഒന്നാം ഡെറിവെറ്റിവ്. അതായത് \(D\)യുടെ രണ്ടാം ഡെറിവെറ്റിവ്.)
ആക്സലറേഷന് ആയി. ഇനി ഫോര്സ്:
ന്യൂട്ടന്റെ ഗ്രാവിറ്റെഷന് സമവാക്യം തന്നെ എടുക്കാം.
\[F = - \frac{mMG}{D^2}\]ഇവിടെ:
\(m\) – പാര്ടിക്ക്ള് അല്ലെങ്കില് ഗാലക്സിയുടെ മാസ്
\(M\) – നാം വരച്ച സ്ഫിയറിന് ഉള്ളില് ഉള്ള മാസ്
\(D\) – ഒറിജിനും പാര്ടിക്ക്ള് അല്ലെങ്കില് ഗാലക്സിയും തമ്മിലുള്ള അകലം
\(G\) – ഗ്രാവിറ്റെഷണല് കോണ്സ്റ്റന്റ്
നെഗറ്റിവ് സൈന് ഈ ഫോര്സ് അട്ട്രാക്ട്ടിവ് ആണെന്ന് സൂചിപ്പിക്കുന്നു.
ഫോര്സും ആക്സലറേഷനും തമ്മില് എന്താണ് ബന്ധം?
\[F = m a\]അപ്പോള് \(a\) എന്നത്:
\[a = \frac {F}{m}\]അതായത്:
\[a = - \frac{MG}{D^2}\]ഇതിനെ നാം നേരത്തെ എഴുതിയ ആക്സലറേഷന്റെ സമവാക്യത്തിന് തുല്യം ആക്കാം:
\[a = - \frac{MG}{D^2} = \ddot a(t) R\]ഇങ്ങനെ പോയാല് എവിടെ എത്തും എന്ന് നോക്കാം!
മുകളില് പറഞ്ഞതിനെ ഒന്നുകൂടെ എഴുതാം:
\[\ddot a(t) R = - \frac{MG}{D^2}\]ഇതില് \(D\) എന്നത് \(a(t) R\) ആണെന്ന് നമുക്ക് അറിയാം.
അപ്പോള്:
\[\ddot a(t) R = - \frac{MG}{a^2R^2}\]രണ്ടു വശങ്ങളും \(R\) കൊണ്ട് ഹരിച്ചാല്:
\[\ddot a = - \frac{MG}{a^2R^3}\]രണ്ടു വശങ്ങളും \(a\) കൊണ്ട് ഹരിച്ചാല്:
\[\frac{\ddot a}{a} = - \frac{MG}{a^3R^3}\]ഇനി, ഈ സ്ഫിയറിന്റെ വോള്യം എന്താണ്?
\[Volume = \frac {4}{3} \pi a^3 R^3\]മുകളില് എഴുതിയ \(\frac{\ddot a}{a}\) എന്ന സമവാക്യത്തിന്റെ വലതു ഭാഗത്തെ \( \frac {\frac {4}{3} \pi}{\frac {4}{3} \pi}\) കൊണ്ട് ഗുണിക്കാം:
\[\frac{\ddot a}{a} =- \frac{MG \frac{4}{3} \pi}{\frac{4}{3} \pi a^3R^3}\]ഇപ്പോള് ഡിനോമിനേറ്റര് എന്നത് വോള്യം ആയല്ലോ.
ന്യൂമറേറ്ററില് ഒരു മാസ് \(M\) ഘടകവും ഉണ്ട്.
മാസ് പെര് വോള്യം എന്നത് എന്താണ്?
ഡെന്സിറ്റി.
അപ്പോള് നമുക്ക് മുകളില്പ്പറഞ്ഞ സമവാക്യത്തെ ഇങ്ങനെ എഴുതാം:
(\(\rho\) എന്നത് ഡെന്സിറ്റി ആണെന്ന് ഓര്ക്കുക)
ഇവിടെ ഒരു കാര്യം ശ്രദ്ധിക്കുക: ഈ സമവാക്യത്തില് \(R\) എന്ന ഘടകം അപ്രത്യക്ഷം ആയി. അതായത് ഡെന്സിറ്റി \(R\)നെ പരിഗണിക്കുന്നില്ല. എന്നുവെച്ചാല് നമ്മള് ഏതു ഗാലക്സി എടുത്താലും നാം മുകളില് പറഞ്ഞ സമവാക്യത്തില് എത്തിച്ചേരും. എത്ര ദൂരത്തുള്ള ഗാലക്സി ആയാലും. നമ്മള് എവിടെയാണ് എന്നതും ഈ സമവാക്യം പരിഗണിക്കുന്നില്ല. ഒരു യതാര്ത്ഥ ഐസോട്രോപിക് സിസ്റ്റം ആണ് ഇത്.
ചില പ്രധാനപ്പെട്ട നിരീക്ഷണങ്ങള് ഈ സമവാക്യത്തില് നിന്നും മനസിലാക്കാം.
ഒന്നാമതായി, സ്റ്റാറ്റിക്ക് ആയ ഒരു പ്രപഞ്ചം സാധ്യമല്ല എന്ന് ഈ സമവാക്യം പറയുന്നു. സ്റ്റാറ്റിക്ക് എന്ന് വെച്ചാല് സ്കെയില് ഫാക്ടര് \(a \) സമയത്തിനനുസരിച്ച് മാറുന്നില്ല എന്ന്.
ശൂന്യമല്ലാത്ത ഒരു പ്രപഞ്ചം ഒരിക്കലും സ്റ്റാറ്റിക്ക് ആകില്ല.
ഈ അനുമാനത്തില് എങ്ങനെ എത്തി?
മുകളില് പറഞ്ഞ സമവാക്യത്തിന്റെ വലതു ഭാഗത്ത് \(\rho\) ഉണ്ടല്ലോ. അതായത് ഡെന്സിറ്റി.
സമവാക്യത്തിന്റെ ഇടത് ഭാഗത്ത് \(\frac{\ddot a}{a}\). എന്താണ് ഇത്?
\(\frac{\ddot a}{a}\) എന്നത് സ്കെയില് ഫാക്ടര് \(a \)യുടെ “ആക്സലറേഷന്” പെര് സ്കെയില് ഫാക്ടര് \(a \).
ഇടത് വശം പൂജ്യം ആകണമെങ്കില് വലതു വശത്തുള്ള \(\rho\) പൂജ്യം ആകണം.
അതായത് ശൂന്യമായ പ്രപഞ്ചത്തില് മാത്രമേ സ്കെയില് ഫാക്ടര് \(a \) മാറാതെ ഇരിക്കൂ.
നാം ജീവിക്കുന്ന പ്രപഞ്ചം സ്റ്റാറ്റിക്ക് അല്ലാ എന്നതിന് ഉള്ള ഒരു സൂചനയാണ് ഇത്.
മുകളിലേക്ക് എറിഞ്ഞ കല്ല്
ഒരു കല്ല് എടുത്ത് മുകളിലേക്ക് എറിഞ്ഞു.
അതിന് എന്ത് സംഭവിക്കും?
എറിഞ്ഞതിന്റെ ശക്തി അനുസരിച്ച് ആ കല്ല് കുറച്ചു ദൂരം മേല്പ്പോട്ടു പോകും. എന്നിട്ട് തിരിച്ചു ഭൂമിയില് വീഴും.
ഇതിനെ വിവരിക്കുന്ന സമവാക്യം നമുക്ക് എഴുതി നോക്കാം.
രണ്ടു തരം സമവാക്യങ്ങള് നമുക്ക് എഴുതാം – ന്യൂട്ടന്റെ ചലന നിയമങ്ങളുടെ സമവാക്യം, എനര്ജി കണ്സര്വേഷന് സമവാക്യം.
നമുക്ക് എനര്ജി കണ്സര്വേഷന് സമവാക്യം ആകും കൂടുതല് ഉപയോഗപ്രദം. അതിനാല് ഇത് എഴുതാം.
ഈ കല്ലിന്റെ എനര്ജി എന്നത് അതിന്റെ കിനറ്റിക്ക് എനര്ജിയുടെയും പൊട്ടന്ഷ്യല് എനര്ജിയുടെയും ആകെ തുകയാണ്.
അതായത്:
\[E= \frac {1}{2}mV^2 - \frac{mMG}{x}\]ഇവിടെ,
\( \frac {1}{2}mV^2\) എന്നത് കിനറ്റിക്ക് എനര്ജി
\(\frac{mMG}{x} \) എന്നത് പൊട്ടന്ഷ്യല് എനര്ജി
ഈ ടോട്ടല് എനര്ജി എന്നത് പോസിറ്റിവ് ആകാം അല്ലെങ്കില് നെഗറ്റിവും ആകാം.
ഉദാഹരണത്തിന് ഈ കല്ല് അല്ലെങ്കില് പാര്ട്ടിക്ക്ള് റസ്റ്റ് പൊസിഷനില് ആണെങ്കില് അതിന്റെ വെലോസിറ്റി പൂജ്യമായിരിക്കും. അപ്പോള് എനര്ജി നെഗറ്റിവും.
ഈ കല്ലിന്റെ വെലോസിറ്റി വളരെ കൂടുതലാണ് എന്ന് വെക്കുക. മുകളില് പറഞ്ഞ സമവാക്യത്തിലെ രണ്ടാമത്തെ ഭാഗമായ പൊട്ടന്ഷ്യല് എനര്ജിയെക്കാള് കൂടുതലാണ് വെലോസിറ്റി എങ്കില്, മൊത്തം എനര്ജി പോസിറ്റിവ് ആയിരിക്കും. മൊത്തം എനര്ജി പോസിറ്റിവ് ആണെങ്കില്, ആ കല്ല് അല്ലെങ്കില് പാര്ട്ടിക്ക്ള് തിരിച്ചു ഭൂമിയിലേക്ക് വരില്ല.
ചുരുക്കിപ്പറഞ്ഞാല്:
-
\(E \) പോസിറ്റിവ് ആണെങ്കില് കല്ല് തിരിച്ചു വരില്ല
-
\(E \) നെഗറ്റിവ് ആണെങ്കില് കല്ല് തിരിച്ചു വരും
-
\(E \) പൂജ്യം ആണെങ്കിലോ?
\(E \) പൂജ്യം ആകുന്ന സമയത്ത് കല്ലിനു ഉണ്ടായിരിക്കുന്ന വെലോസിറ്റി ഒരു പ്രത്യേക പേരില് അറിയപ്പെടുന്നു - എസ്കേപ് വെലോസിറ്റി \(V_E\).
\(V_E\)യെ നമുക്ക് കണക്കാക്കി നോക്കാം:
\[\frac {1}{2}mV^2 - \frac{mMG}{x}=0\] \[\frac {1}{2}V^2 - \frac{MG}{x}=0\] \[V^2 = \frac{2MG}{x}\] \[V = \sqrt{\frac{2MG}{x}}\]ഇപ്പറഞ്ഞത് പോലെ, പ്രപഞ്ചത്തിന്റെ വികാസത്തിന്റെ തോതും മൂന്നു തരത്തില് ആകാം:
• എസ്കേപ് വെലോസിറ്റിയെക്കാള് കൂടുതല്
• എസ്കേപ് വെലോസിറ്റിയെക്കാള് കുറവ്
• എസ്കേപ് വെലോസിറ്റിക്ക് തുല്യം
എസ്കേപ് വെലോസിറ്റിയെക്കാള് കൂടുതലാണ് വികാസത്തിന്റെ തോത് എങ്കില് പ്രപഞ്ചം വികസിച്ചുകൊണ്ടേ ഇരിക്കും. ഒരിക്കലും തിരിച്ചു ചുരുങ്ങില്ല.
എസ്കേപ് വെലോസിറ്റിയെക്കാള് കുറവാണ് വികാസത്തിന്റെ തോത് എങ്കില് പ്രപഞ്ചം കുറച്ചു കഴിയുമ്പോള് തിരിച്ചു ചുരുങ്ങി പോകും.
എസ്കേപ് വെലോസിറ്റിക്ക് തുല്യമാണ് വികാസത്തിന്റെ തോത് എങ്കില് പ്രപഞ്ചം വികസിക്കും, പക്ഷെ അതിന്റെ തോത് കുറഞ്ഞു കുറഞ്ഞു വരും. ചുരുങ്ങില്ല. ഒരു അസിംടോട്ട് പോലെ.
ഇതുവരെ നാം പരിഗണിച്ചത് ചെറിയ \(m \)നെ ആണ്.
ഇനി നമുക്ക് വലിയ \(M \)ന്റെ കാഴ്ചപ്പാടില് നിന്ന് എനര്ജി \(E\) കണക്കു കൂട്ടാം.
മുന്പേ എഴുതിയ പോലെ:
\[\frac {1}{2}mV^2 - \frac {mMG}{x} = E\]ചില കാര്യങ്ങള് ഓര്ക്കുക:
-
\(V = \dot a(t)R\)
-
\(D = a(t)R\)
-
ഇവിടെ \(x \) എന്ന് ഉദ്ദേശിക്കുന്നത് \(D \) തന്നെയാണ്.
അപ്പോള്:
\[\frac {1}{2}m \dot a^2 R^2 - \frac {mMG}{a R} = E\]\(E=0 \) ആകുന്ന കേസ് നോക്കാം. അതായത് എസ്കേപ് വെലോസിറ്റി കേസ്.
\[\frac {1}{2}m \dot a^2 R^2 - \frac {mMG}{a R}=0\]\(m\)നെ കളയാം:
\[\frac {1}{2} \dot a^2 R^2 - \frac {MG}{a R}=0\]2 കൊണ്ട് ഗുണിക്കാം:
\[\dot a^2 R^2 - \frac {2MG}{a R}=0\]നമ്മുടെ ലക്ഷ്യം ഒരു ഡെന്സിറ്റിയുടെ ഘടകം കൊണ്ടുവരിക എന്നതാണ്.
ഡെന്സിറ്റി എന്നാല് മാസ് പെര് വോള്യം. മാസ് \(M \) എന്ന ഘടകം ന്യൂമറേറ്ററില് ഉണ്ട്. ഡിനോമിനെറ്ററില് പക്ഷെ \(a^3 R^3\) വരുത്തണം.
ആദ്യം \(R^2\) കൊണ്ട് ഹരിക്കാം:
\[\dot a^2 - \frac {2MG}{a R^3}=0\]ഇനി \(a^2\) കൊണ്ട് ഹരിക്കാം:
\[\frac {\dot a^2}{a^2} - \frac {2MG}{a^3 R^3}=0\]സ്ഫിയറിന്റെ വോള്യം എന്നത് \( \frac {4}{3} \pi a^3 R^3 \) ആണല്ലോ.
അപ്പോള്, നമുക്ക് \( \frac {4}{3} \pi \)നെ കൊണ്ട് ഗുണിച്ച് ഹരിക്കാം!
\[\frac {\dot a^2}{a^2} - \frac {2MG \frac {4}{3} \pi }{ \frac {4}{3} \pi a^3 R^3}=0\]നമുക്കറിയാം \( \frac{M}{\frac {4}{3} \pi a^3 R^3 } \) എന്നത് ഡെന്സിറ്റി \( \rho \) ആണെന്ന്.
അപ്പോള്:
\[\frac {\dot a^2}{a^2} - 2G \rho \frac {4}{3} \pi =0\]അതായത്:
\[\frac {\dot a^2}{a^2} = 2G \rho \frac {4}{3} \pi\]അല്ലെങ്കില്:
\[\frac {\dot a^2}{a^2} = \frac {8}{3} \pi G \rho\]സ്റ്റാന്ഡേര്ഡ് ഫോമില് ആക്കുകയാണെങ്കില്:
ഇതാണ് ഫ്രീഡ്മന് സമവാക്യം – ന്യൂട്ടോണിയന് കാഴ്ചപ്പാടില്.
ഈ സമവാക്യത്തെ സോള്വ് ചെയ്യാം.
നമുക്കറിയാം \( \rho = \frac {\nu}{a^3}\)
(\( \nu\) എന്നത് ഒരു യൂണിറ്റ് ഗ്രിഡിനുള്ളില് ഉള്ള മാസ് ആണെന്ന് ഓര്ക്കുക.)
അപ്പോള് നമുക്ക് മുകളില് പറഞ്ഞ സമവാക്യത്തെ ഇങ്ങനെ എഴുതാം:
\[\left( \frac {\dot a}{a}\right)^2 = \frac {8}{3} \pi \frac {\nu G}{a^3}\]വലതു വശത്ത് \(a \) ഒഴിച്ച് ഉള്ളവയെല്ലാം കോണ്സ്റ്റന്റുകളാണ്.
\(\left( \frac {\dot a}{a}\right)^2\) എന്ന ഘടകം എങ്ങനെ ബിഹേവ് ചെയ്യുന്നു എന്നതാണ് നമ്മുടെ വിഷയം.
അതിനാല് നമുക്ക് ഈ സമവാക്യത്തെ എളുപ്പത്തിനായി ഇങ്ങനെയും എഴുതാം:
\[\left( \frac {\dot a}{a}\right)^2 \approx \frac{1}{a^3}\]ഈ സമവാക്യം ഒരിക്കലും നെഗറ്റിവ് ആകില്ല എന്ന് ശ്രദ്ധിക്കുക. എന്തുകൊണ്ട്? കാരണം ഇടതുവശം ഒരു സ്ക്വയര് ആണ്.
മറ്റൊരു കാര്യം: വലതു ഭാഗം പൂജ്യം ആകുമോ?
ഇല്ല.
\(a\) വലുതാകുന്നതനുസരിച്ച് \(\frac{1}{a^3}\) ചെറുതായി ചെറുതായി വരും പക്ഷെ പൂജ്യത്തില് എത്തില്ല.
\(\frac {\dot a}{a}=0\) എന്നത് പ്രപഞ്ചം വികസിക്കുന്നത് നിന്നിട്ട് തിരിച്ചു ചുരുങ്ങാന് ആരംഭിക്കുന്ന സന്ദര്ഭം ആണ്.
ഇനി നമുക്ക് ഇതിന്റെ സൊല്യൂഷന് കണ്ടുപിടിക്കാം.
ആദ്യം രണ്ടു വശത്തിന്റെയും സ്ക്വയര് റൂട്ട് എടുക്കുക:
\[\frac {\dot a}{a} = \frac{1}{a \sqrt a}\]രണ്ടു വശവും \(a\) കൊണ്ട് ഗുണിച്ചാല്:
\[\dot a = \frac {1}{\sqrt a}\]അതായത്:
\[\frac {da}{dt} = \frac {1}{\sqrt a}\]ഇനി, \(\frac {da}{dt}\) എന്നാല് എന്താണ്? \(t\)ക്ക് അനുസരിച്ച് \(a\)ക്ക് ഉണ്ടാകുന്ന മാറ്റം.
ഒരു ട്രിക്ക് ചെയ്യാം. ഇതിനെ ഇങ്ങനെ ചിന്തിക്കുന്നതിനു പകരം, ഫ്ലിപ്പ് ചെയ്യാം.
അതായത്, \(\frac {dt}{da}\). \(a\)ക്ക് അനുസരിച്ച് \(t\)ക്ക് ഉണ്ടാകുന്ന മാറ്റം.
\[\frac {dt}{da} = \sqrt a\]ഏതു ഫങ്ങ്ഷനാണ് \(\sqrt a\) എന്ന ഡെറിവേറ്റിവ് ഉള്ളത്?
ഉത്തരം: \(\frac{2}{3} a^{\frac{3}{2}}\)
അതായത്:
\[t = \frac{2}{3} a^{\frac{3}{2}}\]മുന്നിലുള്ള \(\frac{2}{3} \)നെ ഇഗ്നോര് ചെയ്യാം.
അപ്പോള്:
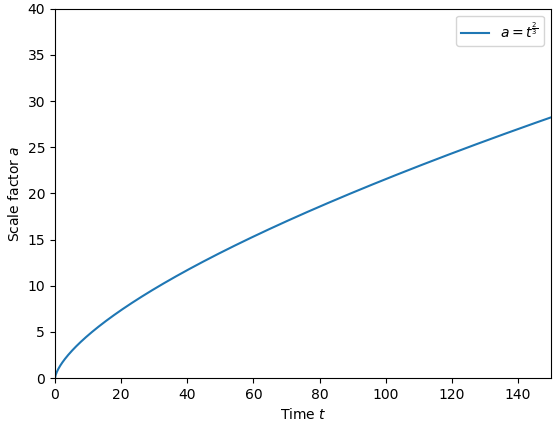
\[a = t^{\frac{2}{3}}\]അതായത് \(a\) എന്നത് സമയം \(t\)യുടെ \(\frac{2}{3}\) പവറിനു ആനുപാതികമായി ആണ് മാറുന്നത്.
ഗ്രാഫ് നോക്കൂ:
നാം പരിഗണിച്ച മറ്റു സാഹചര്യങ്ങളുടെ ഗ്രാഫ്:
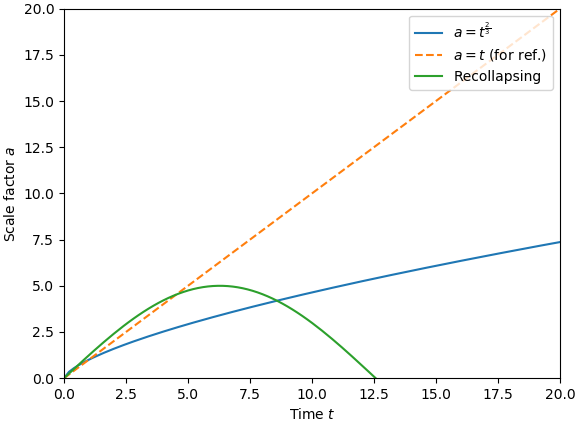
ഇതില് ഓറഞ്ച് നിറത്തില് ഡാഷ് ഇട്ട ലൈന് \(a=t\) എന്ന റിലേഷന് കാണിക്കുന്നു. ഇത് വെറുതെ ഒരു റഫറന്സിന് ആണ് കൊടുത്തിരിക്കുന്നത്.
പച്ച നിറത്തില് ഉള്ള കര്വ്, വികസിച്ച് പിന്നീട് ചുരുങ്ങുന്ന പ്രപഞ്ചത്തെ കാണിക്കുന്നു. മുകളിലേക്ക് എറിഞ്ഞ കല്ലിന്റെ കാര്യം പോലെ.
നീല നിറത്തില് ഉള്ള കര്വ് \(a=t^{\frac{2}{3}}\)നെ കാണിക്കുന്നു. ഈ കര്വ് വലത്തോട്ട് പോകുന്തോറും ചരിവ് കുറഞ്ഞു കുറഞ്ഞു വരുന്നു. പക്ഷെ ഒരിക്കലും ഒരു ഹോറിസോണ്ടല് ലൈന് ആകില്ല.
ഈ നീല കര്വ് പോലെ ആയിരുന്നേനെ നമ്മുടെ പ്രപഞ്ചത്തിന്റെ വികാസവും പരിണാമവും, താഴെ പറയുന്നവ ശരിയായിരുന്നെങ്കില്:
- ന്യൂട്ടന്റെ ചലന നിയമങ്ങള് അടിസ്ഥാനപരം.
- സ്പേസ് ഫ്ലാറ്റ് ആണ്.
- സ്പേസ്, ടൈം എന്നിവ തമ്മില് ബന്ധമില്ല. രണ്ടും ഇന്ഡിപ്പെന്റന്റ്.
- പ്രപഞ്ചത്തില് ദ്രവ്യം മാത്രമേ ഉള്ളൂ.
ഇവയൊന്നും ശരിയല്ല എന്ന് ഇന്ന് നമുക്ക് അറിയാം.
- ന്യൂട്ടന്റെ ചലന നിയമങ്ങള്, ആപേക്ഷികതയുടെ ഒരു പ്രത്യേക കേസ് മാത്രമാണ്.
- സ്പേസ് ഫ്ലാറ്റ് ആകണം എന്നില്ല. സ്പേസില് കര്വേച്ചറുകള് ഉണ്ടാകാം.
- സ്പേസ്, ടൈം എന്നിവ വേര്പെടുത്താനാകാത്ത വണ്ണം ബന്ധപ്പെട്ടിരിക്കുന്നു.
- പ്രപഞ്ചത്തില് ദ്രവ്യം മാത്രമല്ല. മറിച്ച് റേഡിയേഷന്, ഡാര്ക്ക് എനര്ജി, ഡാര്ക്ക് മാറ്റര് എന്നിവ ഉണ്ട്.
അതിനാല് നാം ഇവിടെ ഡിറൈവ് ചെയ്ത ഫ്രീഡ്മന് സമവാക്യം ശരിയല്ല.
പ്രപഞ്ചം മുകളില് കാണിച്ച നീല കര്വ് പോലെയല്ല വികസിക്കുന്നത്.
പിന്നെ ഏതാണ് ശരിക്കുള്ള ഫ്രീഡ്മന് സമവാക്യം?
യഥാര്ത്ഥത്തില് ഒരു ഫ്രീഡ്മന് സമവാക്യം അല്ല ഉള്ളത്. പലതു ഉണ്ട്, ഫ്രീഡ്മന് സമവാക്യങ്ങള്.
അതിലേക്കു പോകുന്നതിനു മുന്പ് നമുക്ക് പ്രപഞ്ചത്തില് ഉള്ള മറ്റുതരം വസ്തുക്കളെ കുറിച്ചും, അവയെക്കൊണ്ടു പ്രപഞ്ചം നിറഞ്ഞിരുന്നാല് ഈ സമവാക്യങ്ങള് എങ്ങനെ മാറും എന്നും എല്ലാം നോക്കാം, അടുത്ത ചാപ്ടറില്.